| Главная » Статьи » это интересно » это интересно |
Математика
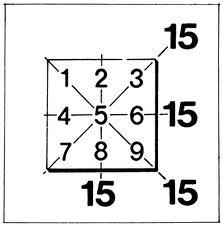 Число — одно из основных понятий математики, возникшее впервые в связи с потребностями счета предметов и совершенствовавшееся затем по мере развития математических знаний. С введением понятий сложения, вычитания, умножения и деления начинает развиваться наука о числах и действиях над ними — арифметика.
Первоначально понятие отвлеченного числа отсутствовало — число было «привязано» к тем предметам, которые пересчитывали, и в языке первобытных народов существовали различные словесные обороты для обозначения одного и того же числа разных предметов. Отвлеченное понятие натурального числа (т. е. числа, не связанного с пересчетом конкретных предметов) появляется и закрепляется вместе с развитием письменности и введением для обозначения чисел определенных символов.
Было время, когда для счета предметов употреблялись лишь два числительных: один и два. В процессе дальнейшего расширения системы счисления привлекались части человеческого тела и в первую очередь пальцы, а если не хватало такого рода «цифр», то еще палочки, камешки и другие вещи.
Н. Н. Миклухо-Маклай в своей книге «Путешествия» рассказывает о забавном способе счета, применявшемся туземцами Новой Гвинеи:
«Излюбленный способ счета состоит в том, что папуас загибает один за другим пальцы руки, причем издает определенный звук, например, «бе, бе, бе» ... Досчитав до пяти, он говорит «ибон-бе» (рука). Затем он загибает пальцы другой руки, снова повторяет «бе, бе» ..., пока не доходит до «ибон-али» (две руки). Затем он идет дальше, приговаривая «бе, бе» ..., пока не доходит до «самба-бе» и «самба-али» (одна нога, две ноги). Если нужно считать дальше, папуас пользуется пальцами рук и ног кого-нибудь другого».
Вслед за возникновением и развитием чисел появилась и замечательная наука об их свойствах и законах, ими управляющих: «теория чисел».
Появление дробных (положительных рациональных) чисел было связано с необходимостью производить измерения, т. е. процедуру, в которой какая-либо величина сравнивается с другой величиной того же рода, выбираемой в качестве эталона (единицы измерения). Но так как единица измерения не всегда укладывалась целое число раз в измеряемой величине, и пренебречь этим обстоятельством в ряде случаев было нельзя, то возникла практическая потребность ввести более «мелкие» числа, нежели натуральные. Это и было источником возникновения наиболее «простых» дробей, таких, как половина, треть, четверть и т. д.
Дальнейшее развитие понятия числа было обусловлено уже не только непосредственной практической деятельностью человека, но и явилось следствием развития математики.
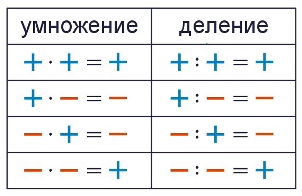 Введение отрицательных чисел было вызвано развитием алгебры как науки, дающей общие способы решения арифметических задач независимо от их конкретного содержания и исходных числовых данных. Отрицательные числа систематически употреблялись индийскими математиками еще в VI—XI веках. В европейской науке отрицательные числа окончательно вошли в употребление лишь после работ Р. Декарта в XVII веке, давшего их геометрическое истолкование.
Множество рациональных чисел оказывается достаточным для удовлетворения большинства практических потребностей — с помощью рациональных чисел измерения можно выполнять с любой наперед заданной степенью точности.
  Старинные русские меры длины
Пядь — это расстояние между вытянутыми большим и указательным пальцами руки при их наибольшем удалении (размер пяди колебался от 19 см до 23 см).
Локоть — это расстояние от конца вытянутого среднего пальца руки до локтевого сгиба (размер локтя колебался в пределах от 38 см до 46 см и соответствовал двум пядям). Большими единицами измерения были простая сажень — расстояние между большими пальцами вытянутых в противоположные стороны рук человека (равнялась примерно 152 см и состояла из 4 локтей или 8 пядей). Большие расстояния в старину измерялись верстами. В переводе на современную систему мер верста межевая равна примерно 2,16 км, сажень — 216 см, аршин — 72 см, а вершок — 4,5 см. Пи-число — число, равное отношению длины окружности к ее диаметру. Пи-число представляется бесконечной десятичной дробью 3,14159265...
Пифагор, VI в. до н. э. (580—500)
 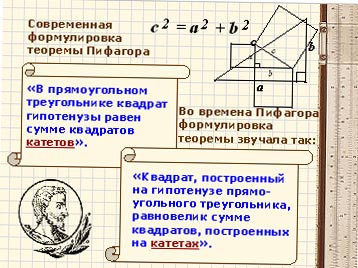 Древнегреческий философ и математик. Первым заложил основы математики как науки, имел свою школу (школа Пифагора). Ему приписывают открытие так называемого правила Пифагора, хотя геометрическая интерпретация этой проблемы была известна и раньше.
Архимед (ок. 287—212 до н. э.)
Величайший учёный Древнего мира. Имя его овеяно легендами. Мы восклицаем: <Эврика!>, — выражая, как Архимед, восторг по поводу своей удачи. Именно он придумал формулу для определения площади треугольника по его сторонам (она известна нам как формула Герона). Не кто иной, как Архимед, первый дерзнул исчислить размеры окружающего нас Мира. Он определил границы для числа π.
Карл Гаусс (1777-1855)
Его математическое дарование проявилось уже в детстве. Рассказывают, что в 3-ёхлетнем возрасте он удивил окружающих, поправив расчёты своего отца с каменщиками. Пока он диктовал задание, у Гаусса уже был готов ответ. Рассказывают, что когда 9-летнему Гауссу учитель предложил найти сумму всех целых чисел от 1 до 100,
1 + 2 + 3 + … + 98 + 99 + 100,
На его грифельной доске было написано: 101*50=5050. маленький Гаусс сам сообразил, каким способом можно очень быстро выполнить это сложение.Надо складывать первое число с последним, второе с предпоследним и т. д. Сумма каждой такой пары чисел равна 101 и повторяется она 50 раз.
Следовательно, сумма всех целых чисел от 1 до 100 будет равна 101 × 50 = 5050.
Блез Паскаль (1623-1662) Французский математик, физик, философ, писатель. Родился в семье юриста, занимающегося математикой. Рано проявил математические способности. Имеет трактат «Опыт о конических сечениях. Сконструировал суммирующую машину. Имеет работы по теории чисел, арифметике, теории вероятностей. Нашёл общий алгоритм для нахождения признаков делимости чисел. Имеет трактат об «Арифметическом треугольнике». Установил принцип действия жидкостей и газов. Написал «Письма к провинциалу»- шедевр французской сатирической прозы.
| |
| Просмотров: 3367 | Рейтинг: 0.0/0 |
| Всего комментариев: 0 | |